问题描述
车辆路径问题同样是一个和实际生活非常接近的问题。问题设定中包含 $M$ 个客户,每个客户有需求 $d_i$ 和所在的位置 $(x, y)$ 。位于起点的仓库可以派出 $N$ 辆送货车,每辆车有最大送货容量 $C$ ,车辆基础成本为 $S$,从 a 点开车到 b 点的成本和距离成正比。车辆要覆盖所有客户的需求,不重不漏,并且优化目标为求最少送货成本、需要的送货车辆数量 $N$,以及每辆车的路径。
局部搜索
由于车辆路径问题变量太多,总车辆数、每辆车负责的客户以及客户的顺序均可以调整,因此即时通过构建整数规划的标准形式并通过工具包求解,效率也不会太高。为了完成作业,这里我们只采用局部搜索的方式解决问题。
局部搜索的资料有很多,这一篇文章和我们要解决的问题非常吻合,因此我们尝试复现文章中设计的搜索方法求解问题。
为了避免歧义,我们先定义一些术语:
- 一辆车从客户 a 直接行驶到客户 b 时,我们称这辆车驶过了一条“边” ( edge )
- 一辆车连续驶过多个客户,即驶过多条首尾相连的边时,我们称这辆车驶过了一段“路径” ( path )
- 一辆车从起点出发,途径所有分配给它的客户,最终回到起点时,我们称这辆车驶过了一条“回路” ( route )
有了这些术语,我们就可以定义四种基本的局部搜索模式了。
路径平移 Shift
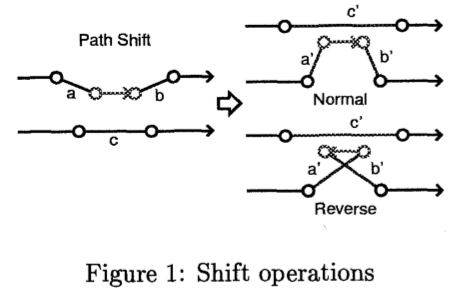
路径平移,就是将一条回路中的部分路径移动到另一条回路中的某个位置,可以正接也可以反接。如果在不违反限制条件的情况下,可以讲一整条回路平移到另一回路中,那也就相当于合并了两条回路,减少了一辆车的需求。
路径交换 Interchange
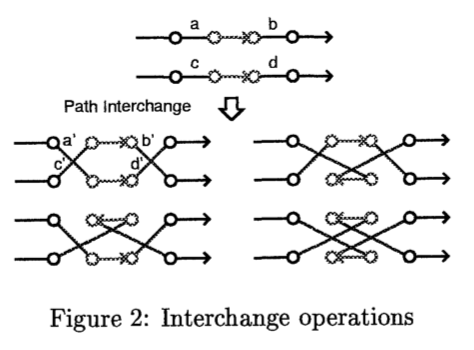
路径交换,与平移类似,就是交换两个回路中各自的两端路径,由于两路径均可以在交换之后正接反接,因此一次交换可以产生四种可能的结果。
回路内换边 2-exchange
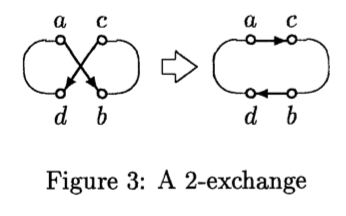
回路内换边,和 TSP 的 2-opt 操作相同,即重新连接一条回路内两条边,进行一个“拧麻花”的操作。
回路间首尾重组 Ladder
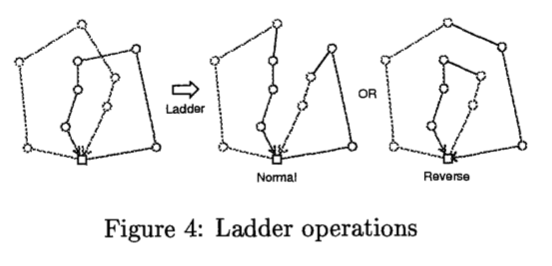
回路间首尾重组,就是在两条回路中各自设置一个断点,将两条回路断点两侧的路径重新连接形成两条新回路。根据首尾连接的方式不同,可以产生两种结果。
搜索初始解
局部搜索在操作过程中,只能在有效解间进行搜索并优化目标函数,因此需要找到一个效果不是很好但是可行的解作为搜索的起点。由于车辆路径问题变量多、关联性强、限制条件多,因此很难直接得到一组可行解。在这里我们采用贪心法得到第一组可行解并开始搜索。
搜索的过程是:每当还有顾客没有覆盖到但当前没有车辆有足够容量时,增加一辆货车,从目前没有被覆盖的需求最小的客户开始送货,直至容量不足。如此操作直至所有客户都被覆盖。这样可以保证每个客户覆盖不重不漏,并且车辆容量都足够。
找到初始解之后,就可以开始进行局部搜索,直至达到最大搜索时间、最大搜索次数或者无法通过局部搜索找到更优解为止。求解代码在这里。