0%

Posted on Edited on

题目要求：

输入两个字符串名叫 needle 和 haystack ，找到 needle 出现在 haystack 中的位置，如果没有出现则返回 -1 。字符串取名出自英语的 Needle in a haystack 即“大海捞针”。

思路：

对于这样的问题，高级算法如 KMP 可以把复杂度控制在 $O(m+n)$ 。但是 KMP 极难理解，也很难在面试中一次写出不出 bug 。因此，解决这个问题时用比较朴素的比较算法即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution(object):
    def strStr(self, haystack, needle):
        """
        :type haystack: str
        :type needle: str
        :rtype: int
        """
        if haystack is None or needle is None:
            return -1
        l1 = len(needle)
        l2 = len(haystack)
        if l1 == 0 or haystack == needle:
            return 0
        elif l1 > l2:
            return -1
        for i in range(l2 - l1 + 1):
            if haystack[i:i + l1] == needle:
                return i
        return -1

Posted on Edited on

题目要求：

输入数组和一个目标数字，要求从数组中原位去掉全部目标数字，并返回新数组长度，不要使用额外的存储空间。

思路：

与 Leetcode 026 Remove Duplicates from Sorted Array 思路一致。采用快慢指针，快指针遍历数组，慢指针从零开始，遇到非目标数字时将快指针的数值复制到慢指针处，慢指针前进一位。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution(object):
    def removeElement(self, nums, val):
        """
        :type nums: List[int]
        :type val: int
        :rtype: int
        """
        if nums is None or nums == []:
            return 0
        if val not in nums:
            return len(nums)
        slow, fast = 0, 0
        for fast, fast_val in enumerate(nums):
            if fast_val == val:
                continue
            else:
                nums[slow] = nums[fast]
                slow += 1
        return slow

Posted on Edited on

题目要求：

输入一个有序，并且可能含有重复内容的数组，原位删除重复内容，空间复杂度为常数级别，并返回无重复数组长度。无重复部分之外内容不限。

思路：

快慢指针，快指针遍历数组，慢指针从零开始，每当遇到一个新数字时将新数字复制到当前慢指针位置并前进一位，最后返回慢指针位置加 1 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution(object):
    def removeDuplicates(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if len(nums) <= 1:
            return len(nums)
        l = len(nums)
        slow = 0
        for fast in range(l):
            if nums[fast] != nums[slow]:
                slow += 1
            nums[slow] = nums[fast]
        return slow + 1

Posted on Edited on

题目要求：

输入一个单向链表，对相邻的两个节点进行交换。如输入 1->2->3->4 输出 2->1->4->3

思路：

在开始时在链表头部建立一个额外的辅助节点，用 p 指向它。对每一对链表节点，用 q 标记出来保护引用位置不至于丢失。之后交换两个节点和相应的连接即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution(object):
    def swapPairs(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        if head is None or head.next is None:
            return head
        placeHolder=ListNode(0)
        placeHolder.next=head
        p=placeHolder

        while p.next and p.next.next:
            q=p.next.next
            p.next.next=q.next
            q.next=p.next
            p.next=q
            p=p.next.next
        return placeHolder.next

Posted on Edited on

题目要求：

输入多个排好序的链表，合并成一个排好序的链表。

思路：

因为每个链表已经排好序，所以可以采用堆排序加快合并速度。首先将各个链表的表头值和链表编号放入最小堆，按表头值排序。每次取出一个最小值，将其对应的表头放入合并后的链表，并将对应编号的链表的表头向后移动一个位置，再将新表头值和编号放回最小堆。直至所有链表表头均为空，合并完毕。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution(object):
    def mergeKLists(self, lists):
        """
        :type lists: List[ListNode]
        :rtype: ListNode
        """
        if lists is None or lists == []:
            return None
        mergeCache = []
        p = ListNode(None)
        q = p

        for i in range(len(lists)):
            if lists[i]:
                heapq.heappush(mergeCache, (lists[i].val, i))

        while mergeCache:
            val, head_i = heapq.heappop(mergeCache)
            q.next = lists[head_i]
            q = q.next
            lists[head_i] = lists[head_i].next
            if lists[head_i]:
                heapq.heappush(mergeCache, (lists[head_i].val, head_i))

        return p.next

Posted on Edited on

XKCD comic about password strength
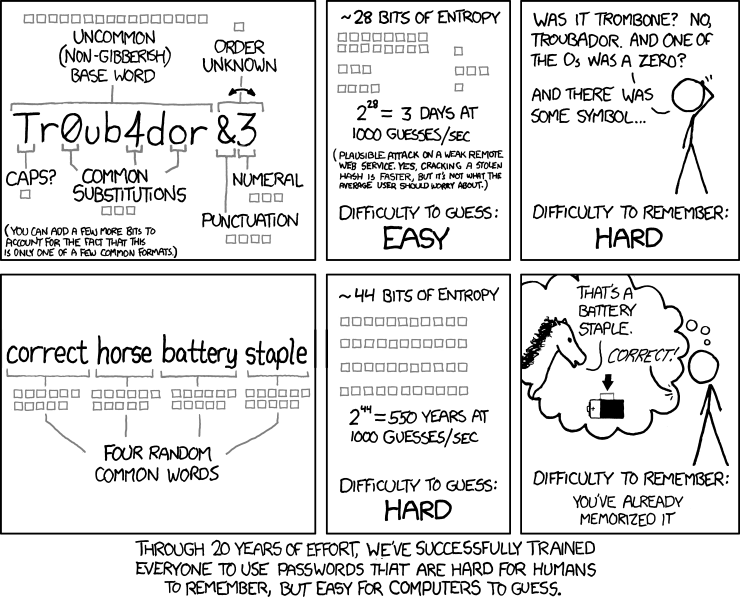
Diceware是一种生成便于记忆并难以通过暴力穷举密码的方式。很长时间以来，网站都在建议人们使用更加复杂的密码，如：

  • 混合使用大小写字母和数字
  • 使用标点符号
  • 避免出现常见单词的拼写组合
  • 在不同的网站使用不同的密码以避免被撞库

几种常见的密码组合方式的组合数分别为：

密码成分 8位组合数 12位组合数 16位组合数
a-z $10^{11.3}$ $10^{17.0}$ $10^{22.6}$
a-z0-9 $10^{12.5}$ $10^{18.7}$ $10^{24.9}$
a-zA-Z $10^{13.7}$ $10^{20.6}$ $10^{27.5}$
a-zA-Z0-9 $10^{14.7}$ $10^{22.0}$ $10^{29.3}$
a-zA-Z0-9& $10^{15.8}$ $10^{23.7}$ $10^{31.6}$

这样的确可以生成复杂度极高的密码，但是这样的密码对用户非常不友好，难以记忆，所以事实上真正这样做的人并不多。毕竟，没有多少人真得能牢记形如 z28>+J]pFF22c+tj 、 ?WtdCW(a9j9u2+jw 、 @^xtE9am#(eFC9H8 、 T3sY]7]tnRc28U>} 、 i949re{NCjje%/*9 的密码，并且能分清分别对应哪个网站、哪个账户。

用 Diceware 生成密码可以在一定程度上解决这个问题。 Diceware 的原理是：对字典中的每一个单词用长度一定（如5位）的6进制数字编号，生成密码时，掷一枚均匀的六面骰子5次，得到一个5位的6进制数字，根据编号找到并记录这个单词。重复这样的操作3到5次，即可得到长度为3至5个单词的diceware密码。可以针对这几个单词编一个故事便于记忆。

电子前线基金会（EFF）在网站上给出了一个已经完成编号的单词列表，其中包含了 $6^5=7776$ 个单词，另外，在 github 上还可以找到包含近50万单词的词汇列表。根据 EFF 的词典生成的随机密码可以具有相当高的复杂度：

  • 随机选取3个单词一共有 $(6^5)^3=10^{11.7}$ 种不同的组合
  • 随机选取4个单词一共有 $(6^5)^4=10^{15.6}$ 种不同的组合
  • 随机选取5个单词一共有 $(6^5)^5=10^{19.5}$ 种不同的组合

相对于记住十几位毫无规律的随机字符串，通过编故事记住几个形如 aloft-applied-embody 、 mug-gown-getaway 、 idiom-eggnog-sadden 的单词组合应该会容易的多。

利用 Python ，写一个生成 Diceware 密码的程序非常简单：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import collections
import random

diceware = collections.defaultdict()

with open('eff_large_wordlist.txt') as fp:
    for line in fp:
        words = line.split()
        diceware[words[0]] = words[1]

length = 3
sep = '-'

words = []
for j in range(length):
    index = "".join([str(random.randint(1,6)) for i in range(5)])
    words.append(diceware[index])
print(sep.join(words))

生成密码的部分还可以分别一行写完

1
print(sep.join([diceware["".join([str(random.randint(1,6)) for i in range(5)])] for j in range(length)]))

另外在实际应用中，要使用密码学安全伪随机数生成器（CSPRNG）

Posted on Edited on

Coursera 是由斯坦福大学的教授吴恩达（Andrew Ng）和达芙妮·科勒联（Daphne Koller）合创建的一个营利性的教育科技公司，与很多大学都有合作。经过几个月的尝试，我终于在昨天晚上通过了Coursera 上由墨尔本大学提供的Discrete Optimization这一门课，拿到了课程认证。虽然最终的成绩离满分还很远，但是我觉得把我在解决作业问题中的思路记录下来是有一定意义的。我的作业代码保存在了 github 上，欢迎 star 、 fork 、发 pull request 。

背包问题的描述

假设我们有一个容量为 $K$ 的背包，以及 $n$ 个物品，每个物品有重量 $w_i$ 和价格 $v_i$ ，题目的目的是找到一个背包可以装下的物品组合（总体积不超过背包容量），并且总价格最高。

在作业中，输入数据为背包总容量 cap 和物品列表 items 每个物品有 value 、 weight 、 density 三个属性。输出数据为背包总价值 value 以及长度等于 items 的数组 taken ，其中元素为 1 则表示对应物品放入背包中，否则不放。

背包问题是NP完全问题，不存在“高效”的多项式时间的最优解法，但是可以通过动态规划实现比较高效的解法，或者用整数规划软件包高速求解。

朴素解法

求解背包问题最朴素的办法就是尝试所有可能的物品组合，找到符合要求的最优解。由于每个物品有两种状态，即放进背包和不放进背包，因此朴素解法需要尝试 $2^n$ 种不同的组合才能保证找到最优解，效率极低。

贪心法 （Greedy Algorithm）

贪心法的原理就是在每一步的时候都采取当前状态下最优的选择，并期望最终能达到比较好的结果。这样做的有点是速度快，对于背包问题来讲，无论是基于物品价格的贪心还是价格密度的贪心，只要计算完成就可以不断向背包中添加物品直至无法添加任何一件新物品。缺点则是并不能达到最优，并且性能没有很好的保障，只能得到近似解或次优解。这里以密度贪心算法举例：

1
2
3
4
5
6
7
8
9
10
11
12
13
Item = namedtuple("Item", ['index', 'value', 'weight', 'density'])

def greedy(cap, items):
    n = len(items)
    taken = [0] * n
    filled = 0
    value = 0
    for item in sorted(items, key=attrgetter('density')):
        if filled + item.weight <= cap:
            taken[item.index] = 1
            value += item.value
            filled += item.weight
    return value, 0, taken

动态规划 （Dynamic Programming, DP）

动态规划可以比朴素算法更快地得到背包问题的最优解，但是对于规模较大的问题仍然性能极低并且有极高的内存占用。适用于动态规划的问题需要有这样的性质：

  1. 最优子结构性质：如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）
  2. 无后效性：即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响
  3. 子问题重叠性质：子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率

用动态规划求解背包问题的思路是：

  • 令 $S(k, j)$ 为求容量为 $k$ ，有 $j$ 个可选物品的背包问题最优解的函数
  • 假设已知 $S(k, j-1)$ 的值，即已经解决了容量为 $k$ ，有 $j-1$ 个可选物品的背包问题。在引入第 $j$ 个物品后：
    • 如果 $w_j>k$ 则背包无法放下新物品， $S(k, j)=S(k, j-1)$
    • 否则，比较选择放入 $j$ 和不放 $j$ 的函数值，即 $$S(k, j)=\max(S(k, j-1), v_j+S(k-w_j, j-1))$$ 其中放入 $j$ 时的总价值计算思路是先找 $S(k-w_j, j-1)$ ，该问题已经求解可以直接查表，再加上 $v_j$ 即可
  • 初始化 $S(k, 0)=0$
  • 当 $k=K, j=n$ 即所有物品已经放完，开始从 $S(K, n)$ 开始反向查找确定每个物品是否被选中：
    • 如果 $S(k, j)=S(k, j-1)$ ，说明第 $j$ 个物品没有被选中，从 $S(k, j-1)$ 继续查找
    • 否则，说明被选中，从 $S(k-w_j, j-1))$ 继续查找

这里用一组简单的数据举例：

  • 背包容量 9
  • 三个物品，重量分别为 4、5、2，价值分别为5，6，3
k\j 0 1 2 3
0 0 0 0 0
1 0 0 0 0
2 0 0 0 3
3 0 0 0 3
4 0 5 5 5
5 0 5 6 6
6 0 5 6 8
7 0 5 6 9
8 0 5 6 9
9 0 5 11 11

经过列动态规划表之后，可以看出，最优解选择了前两个物品，包中物品总价值为 11

解题代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Item = namedtuple("Item", ['index', 'value', 'weight', 'density'])

def dp(cap, items):
    n = len(items)
    taken = [0] * n
    values = [[0 for j in range(cap + 1)] for i in range(n + 1)]
    for i in range(n + 1):
        if i > 0:
            value = items[i - 1].value
            weight = items[i - 1].weight
        for j in range(cap + 1):
            if i == 0 or j == 0:
                continue
            elif weight > j:
                values[i][j] = values[i - 1][j]
            else:
                vTake = values[i - 1][j - weight] + value
                vKeep = values[i - 1][j]
                values[i][j] = max(vTake, vKeep)

    totalWeight = cap
    for i in reversed(range(n)):
        if values[i][totalWeight] == values[i + 1][totalWeight]:
            continue
        else:
            taken[i] = 1
            totalWeight -= items[i].weight

    return values[-1][-1], 1, taken

整数线性规划 （Integer Linear Programming, ILP）

背包问题的设定非常适合转换成 ILP 的标准形式之后用软件包直接求解。在上课的过程中，我发现了 Gurobi 这个数值优化神器，性能极高并且可以让在校生免费使用，并且具有非常简单易用的 python 接口。接下来我们只要根据输入数据对问题进行转换即可。

令 $x_i$ 为优化变量， $x_i=1$ 表示选择第 $i$ 个物品， $x_i=0$ 表示不选择第 $i$ 个物品，可以列出优化问题标准形式如下：
$$\begin{align}
\max & \sum x_i v_i \
s.t. & \sum w_i\leq K\
& x_i\in{0,1}
\end{align}$$

解题时，将问题数据转换成 Gurobi 所需的格式即可直接求解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def mip(cap, items, verbose=False, num_threads=None):
    item_count = len(items)
    values = [item.value for item in items]
    weights = [item.weight for item in items]

    m = Model("knapsack")
    m.setParam('OutputFlag', verbose)
    if num_threads:
        m.setParam("Threads", num_threads)
    else:
        m.setParam("Threads", cpu_count())

    x = m.addVars(item_count, vtype=GRB.BINARY, name="items")
    m.setObjective(LinExpr(values, [x[i] for i in range(item_count)]), GRB.MAXIMIZE)
    m.addConstr(LinExpr(weights, [x[i] for i in range(item_count)]), GRB.LESS_EQUAL, cap, name="capacity")

    m.update()
    m.optimize()

    if m.status == 2:
        opt = 1
    else:
        opt = 0
    return int(m.objVal), opt, [int(var.x) for var in m.getVars()]

TODO

  • 增加贪心法性能边界的讨论
  • 分析常见的 ILP 解法思路

Posted on Edited on

题目要求：

输入整数 n 要求输出所有合理的由 n 对括号组成的字符串。

思路：

采用深度优先搜索（DFS），初始化时左右括号剩余数量均为 n ，搜索中，如果左右括号剩余数均为0，则找到一组解，记录在答案中；如果还剩余左括号，则在当前搜索字符串尾增加一个左括号并继续搜索；同时如果剩余左括号数量小于剩余右括号数量，则在当前搜索字符串尾增加一个右括号并继续搜索，直至所有情况搜索完成，返回答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution(object):
    def generateParenthesis(self, n):
        """
        :type n: int
        :rtype: List[str]
        """
        self.soln = []
        if n == 0:
            return self.soln
        self.dfs(n, n, '')
        return self.soln

    def dfs(self, left, right, s):
        if left == 0 and right == 0:
            self.soln.append(s)
        if left > 0:
            self.dfs(left - 1, right, s + '(')
        if left < right:
            self.dfs(left, right - 1, s+ ')')

Posted on Edited on

题目要求：

给定两个排好序的链表，要求合并成一个新链表，元素来自于两个输入链表并且完成排序。

思路：

用两个指针遍历两个链表，同时新建一个链表，每次对比两个指针所在节点的数字大小，将较小的那个添加到新链表中。当一个链表遍历结束后，直接将另一个链表的全部节点附加到新链表结尾即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution(object):
    def mergeTwoLists(self, l1, l2):
        """
        :type l1: ListNode
        :type l2: ListNode
        :rtype: ListNode
        """
        if not l1 and not l2:
            return None
        elif not l1:
            return l2
        elif not l2:
            return l1
        h = ListNode(None)
        p = h
        while l1 and l2:
            if l1.val < l2.val:
                p.next = ListNode(l1.val)
                l1 = l1.next
            else:
                p.next = ListNode(l2.val)
                l2 = l2.next
            p = p.next
        if not l1:
            p.next = l2
        else:
            p.next = l1
        return h.next

Posted on Edited on

题目要求：

输入一个完全由 '(', ')', '{', '}', '[', ']' 组成的字符串，判定字符串中的括号是不是有效的。

思路：

创建维护一个栈，遍历一遍字符串，遇到左括号时压栈，遇到右括号时，如果栈为空或者弹出的第一个字符不是对应的左括号，返回假。遍历结束没有遇到问题则返回真。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution(object):
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        pstack = []
        pleft = set(['(', '[', '{'])
        for c in s:
            if c in pleft:
                pstack.append(c)
            elif c == ')':
                if pstack == [] or pstack.pop() != '(':
                    return False
            elif c == ']':
                if pstack == [] or pstack.pop() != '[':
                    return False
            elif c == '}':
                if pstack == [] or pstack.pop() != '{':
                    return False
        return len(pstack) == 0